Rethinking What Math Really Is
Math is everywhere. It’s woven into the decisions we make, the patterns we observe, and the problems we solve every day. When students figure out how long their phone battery will last, compare the value of different purchases, or notice the rhythm in their favorite song, they’re thinking mathematically.
Yet in many classrooms, math is often viewed as something much more limited: a subject of right and wrong answers with little space for the kind of exploration and sense-making that students naturally bring. This framing sends a message about who belongs in mathematical spaces and who does not.
Students constantly develop beliefs about who they are as learners. In mathematics, these beliefs shape everything: their willingness to share their thinking, their persistence when facing complex problems, and the opportunities they see for their futures.
Every student should have the chance to develop a mathematical identity that showcases their capabilities, curiosity, and voice. When educators intentionally nurture strong mathematical identities, they equip students with the tools to persist, participate, and thrive. They help students recognize the mathematical thinkers they already are.
Math is about noticing patterns, generalizing those patterns, and then applying them to make decisions in your daily life.
Rolanda Baldwin, VP of Program Design
The Story Students Hear About Math
Students hear it early and often: some people are “math people,” and some aren’t. Sometimes it’s said directly. More often, it’s communicated through which students are called on, whose strategies are shared, or how quickly someone gets additional support. Over time, these messages become a part of how students perceive themselves.
But mathematical thinking is a part of our daily lives, whether we realize it or not. It shows up when we’re planning our time, making sense of information, or solving problems that matter to us. “Math is about noticing patterns, generalizing those patterns, and then applying them to make decisions in your daily life,” says Rolanda Baldwin, Vice President, Program Design. It’s a skill that every student can develop and apply to all aspects of learning and decision-making. When we disconnect “school math” from the mathematical thinking students already engage in, we miss powerful opportunities to show that math has always been part of their toolkit.
The stakes are high. Too often, mathematics acts as a gateway that opens or closes opportunities. “Math has held people back from opportunities, not because they can’t do it, but because of how it was taught and assessed,” Baldwin explains.
Each classroom experience shapes mathematical identity. When students see math as something that welcomes their thinking, they start to feel like they belong. When they’re guided to think independently and understand key mathematical ideas, they develop confidence in their mathematical voice.
Math Makes Better Critical Thinkers and Problem Solvers
Mathematical thinking develops skills that build students’ ability to analyze situations and make informed decisions. When students engage with rich mathematical tasks, they practice strategies that are useful everywhere.
Research by Sachdeva & Eggen demonstrates that working through complex math problems helps students interpret information, evaluate different approaches, and draw logical conclusions. These are the hallmarks of critical thinking that students carry into every area of their learning and daily lives.
Math helps students develop thinking habits that show up at home, at work, and in civic life. They learn to observe carefully, notice structure, and apply what they know to new situations. “What math actually does is develop your ability to be a logical thinker,” Baldwin says. “To evaluate situations, to see structure, to figure out what’s unknown.”
At its heart, math is about patterns: recognizing them, generalizing about them, and using those generalizations to make decisions that matter. When students consider how they can spend money, analyze trends in data affecting their community, or work through scheduling conflicts, they’re applying mathematical thinking in meaningful ways.
This kind of learning sticks because it feels relevant and useful. When we position students as mathematical thinkers rather than answer-producers, we help them develop reasoning skills that transfer across different subjects and situations. That’s the kind of mathematical identity that stays with students long after they leave our classrooms.
Fostering a Positive Math Identity Positively Impacts Student Achievement
When students see themselves as capable mathematical thinkers, they perform differently in learning environments. They’re more likely to share their ideas, take on intellectual challenges, and stay engaged when problems require sustained thinking.
“When they see themselves as capable, they take risks. They’ll try something even if it’s hard,” Baldwin observes.
This willingness to engage with challenging work, or what educators call productive struggle, forms the core of deep mathematical learning. But students only embrace that challenge when they believe their thinking matters and their growth is possible.
Mathematical identity plays a crucial role. Students who feel they belong in mathematical conversations are more likely to ask questions, share their reasoning, and learn from their mistakes. Meanwhile, students who have been positioned as outsiders to mathematical thinking are more likely to disengage from the very experiences that could help them grow.
By fostering positive mathematical identities, educators create conditions where students thrive. Studies confirm this link: students with strong mathematical identities are more likely to persist, engage, and succeed in math-related fields, including STEM pathways.
Students who see themselves as doers of mathematics are more likely to persist through complex tasks, participate actively in class discussions, and carry confidence in their problem-solving abilities into other academic areas.
How To Foster a Positive Math Identity
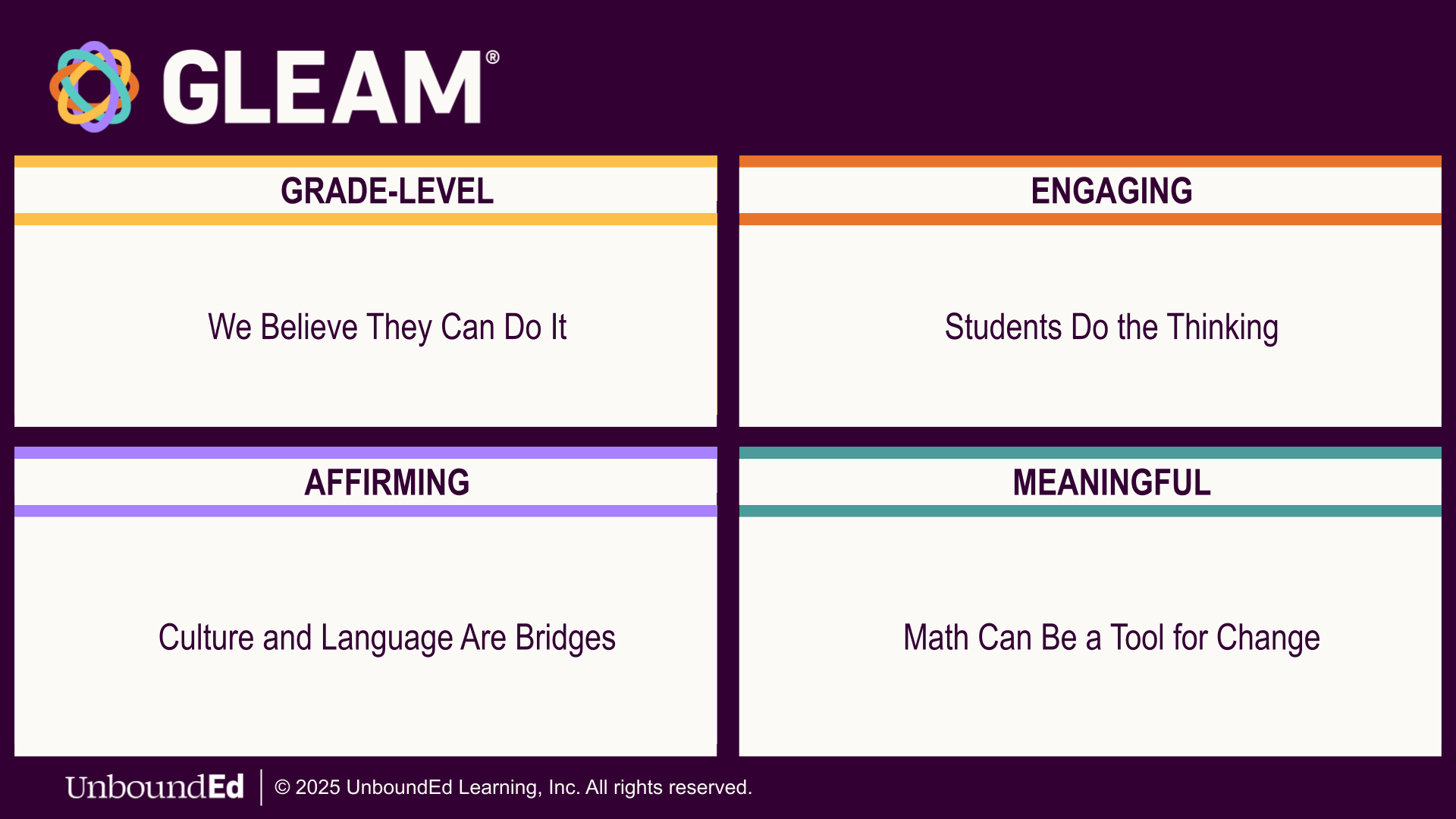
Students not only learn mathematics but also develop as mathematical learners. Their self-perception in that process largely depends on the instructional messages they receive every day.
“This is the work,” educator Baldwin reflects. “It’s the little things. What we say, what we value, how we respond. It all builds up into who students believe they are.”
Students develop strong mathematical identities when they are consistently challenged, affirmed, and invited to understand their learning. This happens through grade-level, engaging, affirming, and meaningful — GLEAM® — instruction.
Every decision educators make can either strengthen or weaken students’ beliefs about themselves as mathematical thinkers. From choosing tasks that honor students’ reasoning to facilitating discussions that value multiple approaches, educators are constantly shaping mathematical identity.
To support educators in this essential work, we’ve developed a practical resource grounded in GLEAM Instruction. Use it to reflect on your current practices, guide team conversations, or plan specific classroom strategies that help every student develop a strong mathematical identity.
Download this resource so it can help you:
- Identify concrete ways to affirm and engage every learner
- Reflect on how daily instructional decisions influence student identity
- Take action toward more student-centered, empowering mathematics classrooms
Fostering Mathematical Identity Through Instruction
When students believe they can do mathematics, they approach learning with curiosity, confidence, and persistence. When they see themselves reflected in what they’re learning and are supported in how they think, they begin to understand that math belongs to them.
This belief doesn’t develop just from motivational posters or encouraging words alone. It grows through the everyday decisions educators make: providing students with access to challenging, grade-level work, honoring their mathematical reasoning, and connecting learning to meaningful contexts for students.
“If kids don’t see themselves in the curriculum, or in the teaching, they disengage,” Baldwin notes. “And when they disengage, their outcomes suffer.”
Mathematical identity shapes more than test scores. It affects how students see themselves as thinkers, as problem-solvers, and as people who can make sense of quantitative information in their world.
This matters because research shows that students with a strong math identity stay engaged longer, achieve more, and are more likely to pursue advanced courses and STEM careers, regardless of where they started.
When their sense of identity is strong and positive, it opens doors to opportunities and possibilities.
Nurturing strong mathematical identities is essential work. It’s how we teach for the futures every student deserves, ensuring that every single student experiences the power and relevance of mathematical thinking, and recognizes the mathematician they’ve always been.